ALAT-ALAT OPTIK
LUP (KACA PEMBESAR)
[sunting]Pembesaran bayangan saat mata berakomodasi maksimum

Dengan ketentuan:
 = Pembesaran
= Pembesaran = Titik dekat (cm)
= Titik dekat (cm)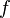 = Fokus lup (cm)
= Fokus lup (cm)
[sunting]Pembesaran bayangan saat mata tidak berakomodasi
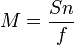
Dengan ketentuan:
 = Pembesaran
= Pembesaran = Titik dekat (cm)
= Titik dekat (cm)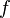 = Fokus lup (cm)
= Fokus lup (cm)
[SUNTING]MIKROSKOP
Pembesaran mikroskop adalah hasil kali pembesaran lensa objektif dan pembesaran lensa okuler, sehingga dirumuskan:

Karena lensa okuler mikroskop berfungsi seperti lup, pembesaran mikroskop dirumuskan sebagai berikut:
[sunting]Pembesaran Mikroskop pada saat mata berakomodasi maksimum

Agar mata berakomodasi maksimum, jarak lensa objektif dan lensa okuler dirumuskan:

Dengan ketentuan:
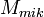 = Pembesaran mikroskop
= Pembesaran mikroskop = Pembesaran oleh lensa objektif
= Pembesaran oleh lensa objektif = Titik dekat mata
= Titik dekat mata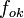 = Jarak fokus lensa okuler
= Jarak fokus lensa okuler = jarak bayangan oleh lensa objektif
= jarak bayangan oleh lensa objektif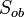 = jarak benda di depan lensa objektif
= jarak benda di depan lensa objektif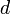 = jarak lensa objektif dan lensa okuler
= jarak lensa objektif dan lensa okuler
[sunting]Pembesaran Mikroskop pada saat mata tidak berakomodasi

Agar mata berakomodasi maksimum, jarak lensa objektif dan lensa okuler dirumuskan:

Dengan ketentuan:
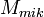 = Pembesaran mikroskop
= Pembesaran mikroskop = Pembesaran oleh lensa objektif
= Pembesaran oleh lensa objektif = Titik dekat mata
= Titik dekat mata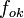 = Jarak fokus lensa okuler
= Jarak fokus lensa okuler = jarak bayangan oleh lensa objektif
= jarak bayangan oleh lensa objektif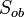 = jarak benda di depan lensa objektif
= jarak benda di depan lensa objektif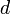 = jarak lensa objektif dan lensa okuler
= jarak lensa objektif dan lensa okuler
[SUNTING]TEROPONG BINTANG
[sunting]Pembesaran Teropong Bintang pada saat mata tidak berakomodasi

Agar mata berakomodasi maksimum, jarak lensa objektif dan lensa okuler dirumuskan:

Dengan ketentuan:
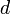 = Jarak lensa objektif dan lensa okuler
= Jarak lensa objektif dan lensa okuler = Pembesaran teropong bintang
= Pembesaran teropong bintang = Jarak fokus lensa objektif
= Jarak fokus lensa objektif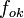 = Jarak fokus lensa okuler
= Jarak fokus lensa okuler
[sunting]Pembesaran Teropong Bintang pada saat mata berakomodasi maksimum

Agar mata berakomodasi maksimum, jarak lensa objektif dan lensa okuler dirumuskan:

Dengan ketentuan:
 = Pembesaran teropong bintang
= Pembesaran teropong bintang = Jarak fokus lensa objektif
= Jarak fokus lensa objektif = jarak benda di depan lensa okuler
= jarak benda di depan lensa okuler
[SUNTING]TEROPONG BUMI
[sunting]Pembesaran Teropong Bumi

Dengan ketentuan:
 = Pembesaran teropong bumi
= Pembesaran teropong bumi = Jarak fokus lensa objektif
= Jarak fokus lensa objektif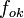 = Jarak fokus lensa okuler
= Jarak fokus lensa okuler
[sunting]Jarak lensa objektif dan lensa okuler
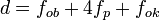
Dengan ketentuan:
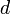 = Jarak lensa objektif dan lensa okuler
= Jarak lensa objektif dan lensa okuler = Jarak fokus lensa objektif
= Jarak fokus lensa objektif = Jarak fokus lensa pembalik
= Jarak fokus lensa pembalik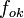 = Jarak fokus lensa okuler
= Jarak fokus lensa okulerDINAMIKA ROTASI
TORSITorsi atau momen gaya adalah hasil kali antara gaya F dan lengan momennya. Torsi dilambangkan dengan lambang .Satuan dari torsi adalah Nm (Newton meter).
.Satuan dari torsi adalah Nm (Newton meter).[SUNTING]MOMEN INERSIA
Momen inersia adalah hasil kali partikel massa dengan kuadrat jarak tegak lurus partikel dari titik poros. Satuan dari momen inersia adalah kg m² (Kilogram meter kuadrat).Besaran momen inersia dari beberapa benda.
Satuan dari momen inersia adalah kg m² (Kilogram meter kuadrat).Besaran momen inersia dari beberapa benda.Benda Poros Gambar Momen inersia Batangsilinder Poros melalui pusat 

Batang silinder poros melalui ujung 

Silinder berongga Melalui sumbu 

Silinder pejal Melalui sumbu 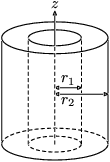
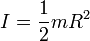
Silinder pejal Melintang sumbu 

Bola pejal Melaluidiameter 

Bola pejal Melalui salahsatu garis singgung 

Bola berongga Melalui diameter 

[sunting]Hubungan antara torsi dengan momen inersia
Hukum II Newton tentang rotasiKeterangan:- I : momen inersia (kg m²)
- α : percepatan sudut (rad/s²)
 : torsi (Nm)
: torsi (Nm)
Subbagian ini akan menjelaskan tentang rumus-rumus yang digunakan pada teori relativitas khusus.
- Kecepatan A menurut B:

Dengan titik O adalah sebuah acuan yang berada diantara A dan B.Keterangan:- VAB: Kecepatan benda A relatif terhadap kecepatan benda B.
- VAO: Kecepatan benda A relatif terhadap acuan O.
- VOB: Kecepatan benda B relatif terhadap acuan O.
- c: kecepatan cahaya (3 x 108 m/s2)
Ada besaran yang gunanya untuk menghitung dilatasi waktu, panjang, dan massa.Dilatasi panjang:Keterangan:
yang gunanya untuk menghitung dilatasi waktu, panjang, dan massa.Dilatasi panjang:Keterangan:- L0: Panjang awal benda.
Dilatasi waktu:Keterangan:- t0: waktu dalam acuan pengamat yang diam.
- t: waktu dalam acuan pengamat yang bergerak.
Dilatasi massa:Energi kinetik relativistik:
TERMODINAMIKA
Hukum Pertama Termodinamika
Perubahan energi dalam: Keterangan:
Keterangan: :Perubahan energi dalam (Joule)
:Perubahan energi dalam (Joule)- U2:Energi dalam pada keadaan akhir (Joule)
- U1:Energi dalam pada keadaan awal (Joule)
Usaha yang dilakukan oleh gas pada tekanan tetap:Keterangan:- p: Besarnya tekanan (atm)
 : Perubahan volume (liter)
: Perubahan volume (liter)
Rumus umum usaha yang dilakukan gas: Penghitungan energi dalam:
Penghitungan energi dalam:- Gas monoatomik:

- Gas diatomik:

[sunting]Proses-proses termodinamika gas
[sunting]Proses isobarik
Proses isobarik adalah perubahan keadaan gas pada tekanan tetap.Persamaan keadaan isobarik: Usaha yang dilakukan pada keadaan isobarik:
Usaha yang dilakukan pada keadaan isobarik: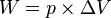
[sunting]Proses isokhorik
Proses isokhorik adalah perubahan keadaan gas pada volume tetap.Persamaan keadaan isokhorik: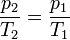
[sunting]Proses isotermis/isotermik
Proses isotermik adalah perubahan keadaan gas pada suhu tetap.Persamaan keadaan isotermik: Usaha yang dilakukan pada keadaan isotermik:
Usaha yang dilakukan pada keadaan isotermik:- Dari persamaan gas ideal

- Rumus umum usaha yang dilakukan gas:
 maka:
maka: karena
karena bernilai tetap, maka:Ingat integral ini!
bernilai tetap, maka:Ingat integral ini!
 maka persamaan di atas menjadimaka menjadi:
maka persamaan di atas menjadimaka menjadi:[sunting]Proses adiabatik
Proses adiabatik adalah perubahan keadaan gas dimana tidak ada kalor yang masuk maupun keluar dari sistem.Persamaan keadaan adiabatik: Tetapan Laplace:
Tetapan Laplace: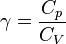 karena
karena , maka persamaan diatas dapat juga ditulis:Usaha yang dilakukan pada proses adiabatik:
, maka persamaan diatas dapat juga ditulis:Usaha yang dilakukan pada proses adiabatik:
TEORI KINETIK GAS
Mol dan massa molekul
1 mol= 6,022 x 1023 molekul6,022 x 1023 juga disebut dengan bilangan avogadro (NA).Massa sebuah atom/molekul: Hubungan antara massa dengan mol:
Hubungan antara massa dengan mol: atau
atau  Keterangan:
Keterangan:- n: jumlah mol
- M: Massa relatif atom/molekul
- m: massa zat (kg)
[sunting]Persamaan keadaan gas ideal
[sunting]Hukum Boyle
Tekanan gas akan berbanding terbalik dengan volumenya pada ruangan tertutup.
[sunting]Hukum Charles Gay-Lussac
Volume benda akan berbanding lurus dengan suhu mutlaknya pada ruangan tertutup.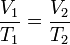 Dari kedua hukum diatas, maka:
Dari kedua hukum diatas, maka: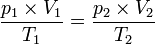 atau disebut dengan Hukum Boyle-Gay Lussac.
atau disebut dengan Hukum Boyle-Gay Lussac.[sunting]Persamaan gas ideal
 Keterangan:
Keterangan:- p: tekanan
- v: volume ruang
- n: jumlah mol gas
- R: tetapan umum gas
- T: suhu (Kelvin)
Perhatikan satuan:- R= 8314 J/kmol K apabila tekanan dalam Pa atau N/m2, volume dalam m3, dan jumlah mol dalam kmol
- R= 0,082 L atm/mol K apabila tekanan dalam atm, volume dalam liter, dan jumlah mol dalam mol
[sunting]Turunan dari persamaan gas ideal
Karena maka dapat dituliskan:
maka dapat dituliskan: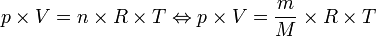

Karena , maka akan didapat persamaan:
, maka akan didapat persamaan: (dari rumus P V = n R T)
(dari rumus P V = n R T)
 , maka:
, maka: k disebut dengan tetapan Boltzmann, yang nilainya adalah:
k disebut dengan tetapan Boltzmann, yang nilainya adalah:
MEKANIKA FLUIDA
Tekanan
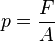 Keterangan:
Keterangan:- p: Tekanan (N/m² atau dn/cm²)
- F: Gaya (N atau dn)
- A: Luas alas/penampang (m² atau cm²)
Satuan:- 1 Pa = 1 N/m² = 10-5 bar = 0,99 x 10-5 atm = 0,752 x 10-2 mmHg atau torr = 0,145 x 10-3 lb/in² (psi)
- 1 torr= 1 mmHg
[sunting]Tekanan hidrostatis

 Keterangan:
Keterangan:- ph: Tekanan hidrostatis (N/m² atau dn/cm²)
- h: jarak ke permukaan zat cair (m atau cm)
- s: berat jenis zat cair (N/m³ atau dn/cm³)
- ρ: massa jenis zat cair (kg/m³ atau g/cm³)
- g: gravitasi (m/s² atau cm/s²)
[sunting]Tekanan mutlak dan tekanan gauge
Tekanan gauge: selisih antara tekanan yang tidak diketahui dengan tekanan udara luar.Tekanan mutlak = tekanan gauge + tekanan atmosfer
[sunting]Tekanan mutlak pada kedalaman zat cair
 Keterangan:
Keterangan:- p0: tekanan udara luar (1 atm = 76 cmHg = 1,01 x 105 Pa)
[sunting]Hukum Pascal
Tekanan yang diberikan pada zat cair dalam ruang tertutup akan diteruskan sama besar ke segala arah. Keterangan:
Keterangan:- F1: Gaya tekan pada pengisap 1
- F2: Gaya tekan pada pengisap 2
- A1: Luas penampang pada pengisap 1
- A2: Luas penampang pada pengisap 2
Jika yang diketahui adalah besar diameternya, maka:
[sunting]Gaya apung (Hukum Archimedes)
Gaya apung adalah selisih antara berat benda di udara dengan berat benda dalam zat cair.
 Keterangan:
Keterangan:- Fa: gaya apung
- Mf: massa zat cair yang dipindahkan oleh benda
- g: gravitasi bumi
- ρf: massa jenis zat cair
- Vbf: volume benda yang tercelup dalam zat cair
[sunting]Mengapung, tenggelam, dan melayang
Syarat benda mengapung: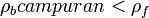 Syarat benda melayang:
Syarat benda melayang: Syarat benda tenggelam:
Syarat benda tenggelam:
Kamis, 26 April 2012
IMPULS dan MOMENTUM
Momentum

 Keterangan:
Keterangan:- p = momentum (kg m/s)
- m = massa benda (kg)
- v = kecepatan benda (m/s)
[sunting]Impuls
Impuls merupakan perubahan momentum. Keterangan:
Keterangan:- I = impuls
 = perubahan momentum (kg m/s)
= perubahan momentum (kg m/s) = perubahan selang waktu (s)
= perubahan selang waktu (s)- F = gaya (Newton)
GETARAN, GELOMBANG DAN BUNYI
Periode dan Frekuensi Getaran
[sunting]Periode Getaran

Dengan ketentuan: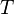 = Periode (sekon)
= Periode (sekon) = Waktu (sekon)
= Waktu (sekon) = Jumlah getaran
= Jumlah getaran
[sunting]Frekuensi Getaran
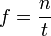
Dengan ketentuan: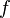 = Frekuensi (Hz)
= Frekuensi (Hz) = Jumlah getaran
= Jumlah getaran = Waktu (sekon)
= Waktu (sekon)
[sunting]Periode Getaran
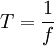
Dengan ketentuan: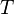 = periode getaran (sekon)
= periode getaran (sekon)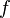 = frekuensi(Hz)
= frekuensi(Hz)
[sunting]Hubungan antara Periode dan Frekuensi Getaran
Besar periode berbanding terbalik dengan frekuensi.Dengan ketentuan: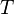 = periode (sekon)
= periode (sekon)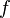 = frekuensi (Hz)
= frekuensi (Hz)
[sunting]Gelombang
[sunting]Gelombang berjalan
Persamaan gelombang:Keterangan:- A: amplitudo (m)
- f: frekuensi (Hz)
 : panjang gelombang (m)
: panjang gelombang (m)
USAHA
Subbab ini akan menjelaskan tentang usaha.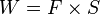
 Keterangan:
Keterangan:- W = usaha (newton meter atau Joule)
- F = gaya (newton)
- S = jarak (meter)
Usaha yang dilakukan oleh pegas:Keterangan:- W = usaha (newton meter atau Joule)
- k = konstanta pegas (Newton/m2)
- x = pertambahan panjang pegas (meter)
TEKANAN
Gaya
Gaya dalam pengertian ilmu fisika adalah seseatu yang menyebabkan perubahan keadaan benda.[sunting]Hukum Newton
[sunting]Hukum I Newton
Setiap benda akan tetap diam atau bergerak lurus beraturan apabila pada benda itu tidak bekerja gaya.
[sunting]Hukum II Newton
Bila sebuah benda mengalami gaya sebesar F maka benda tersebut akan mengalami percepatan.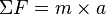 Keterangan:
Keterangan:- F : gaya (N atau dn)
- m : massa (kg atau g)
- a : percepatan (m/s2 atau cm/s2)
[sunting]Hukum III Newton
Untuk setiap gaya aksi, akan selalu terdapat gaya reaksi yang sama besar dan berlawanan arah.
[sunting]Gaya gesek
 Keterangan:
Keterangan:- Fg : Gaya gesek (N)
 : koefisien gesekan
: koefisien gesekan- N : gaya normal (N)
[sunting]Gaya berat
 Keterangan:
Keterangan:- W : Gaya berat (N)
- m : massa benda (kg)
- g : gravitasi bumi (m/s2)
[sunting]Berat jenis
 atau
atau 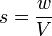 Keterangan:
Keterangan:- s: berat jenis (N/m3)
- w: berat benda (N)
- V: Volume benda (m3)
 : massa jenis (kg/m3)
: massa jenis (kg/m3)
[sunting]Tekanan
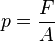 Keterangan:
Keterangan:- p: Tekanan (N/m² atau dn/cm²)
- F: Gaya (N atau dn)
- A: Luas alas/penampang (m² atau cm²)
Satuan:- 1 Pa = 1 N/m² = 10-5 bar = 0,99 x 10-5 atm = 0,752 x 10-2 mmHg atau torr = 0,145 x 10-3 lb/in² (psi)
- 1 torr= 1 mmHg
[sunting]Tekanan hidrostatis

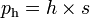 Keterangan:
Keterangan:- ph: Tekanan hidrostatis (N/m² atau dn/cm²)
- h: jarak ke permukaan zat cair (m atau cm)
- s: berat jenis zat cair (N/m³ atau dn/cm³)
- ρ: massa jenis zat cair (kg/m³ atau g/cm³)
- g: gravitasi (m/s² atau cm/s²)
[sunting]Hukum Pascal
Tekanan yang diberikan pada zat cair dalam ruang tertutup akan diteruskan sama besar ke segala arah. Keterangan:
Keterangan:- F1: Gaya tekan pada pengisap 1
- F2: Gaya tekan pada pengisap 2
- A1: Luas penampang pada pengisap 1
- A2: Luas penampang pada pengisap 2
[sunting]Hukum Boyle

ENERGI
Energi mekanik
Energi mekanik adalah jumlah dari energi potensial dan energi kinetik.[sunting]Energi potensial
Energi potensial adalah energi yang dimiliki suatu benda karena memiliki ketinggian tertentu dari tanah. Energi potensial ada karena adanya gravitasi bumi. Dapat dirumuskan sebagai:Keterangan:- Ep: Energi potensial (J)
- m: massa benda (kg)
- g: percepatan gravitasi (m/s2)
- h: tinggi benda dari permukaan tanah (meter)
[sunting]Energi kinetik
Energi kinetik adalah energi yang dimiliki suatu benda karena geraknya. Energi kinetik dipengaruhi oleh massa benda dan kecepatannya.Keterangan:- Ek: Energi kinetik (J)
- m : massa benda (kg)
- v : kecepatan benda (m/s)
[sunting]Energi kinetik pegas
Keterangan:- Ek: Energi kinetik pegas (J)
- k : konstanta pegas (N/m²)
- x : perpanjangan pegas (m)
[sunting]Energi kinetik relativistik

PEMUAIAN
Muai panjang
Rumus:
 = panjang akhir (m, cm)
= panjang akhir (m, cm) = panjang awal (m, cm)
= panjang awal (m, cm) = koefisien muai panjang (/°C)
= koefisien muai panjang (/°C)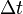 = perbedaan suhu (°C)
= perbedaan suhu (°C)
[sunting]Muai volume
Rumus: Keterangan:
Keterangan: = volume akhir (m3, cm3)
= volume akhir (m3, cm3)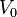 = volume awal (m3, cm3)
= volume awal (m3, cm3) =
=  = koefisien muai volume (/°C)
= koefisien muai volume (/°C)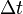 = selisih suhu (°C)
= selisih suhu (°C)
[sunting]Muai luas
Rumus: Keterangan:
Keterangan: = luas akhir (m2, cm2)
= luas akhir (m2, cm2) = luas awal (m2, cm2)
= luas awal (m2, cm2) =
= 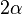 = koefisien muai luas (/°C)
= koefisien muai luas (/°C)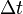 = selisih suhu (°C)
= selisih suhu (°C)
Kamis, 26 April 2012
MASSA JENIS
MASSA JENIS / KERAPATAN JENISρ = m / vKeterangan :- ρ = Massa jenis (kg/m3) atau (g/cm3)
- m = massa (kg atau gram)
- v = volume (m3 atau cm3)
KUMPULAN RUMUS FISIKA
Gerak lurus beraturan
Rumus: Dengan ketentuan:
Dengan ketentuan: = Jarak yang ditempuh (m, km)
= Jarak yang ditempuh (m, km)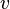 = Kecepatan (km/jam, m/s)
= Kecepatan (km/jam, m/s) = Waktu tempuh (jam, sekon)
= Waktu tempuh (jam, sekon)
Catatan:- Untuk mencari jarak yang ditempuh, rumusnya adalah
 .
. - Untuk mencari waktu tempuh, rumusnya adalah
 .
. - Untuk mencari kecepatan, rumusnya adalah
 .
.
[sunting]Kecepatan rata-rata
Rumus: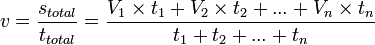
[sunting]Gerak lurus berubah beraturan
Gerak lurus berubah beraturan adalah gerak yang lintasannya berupa garis lurus dengan kecepatannya yang berubah beraturan.Percepatannya bernilai konstan/tetap.Rumus GLBB ada 3, yaitu:Dengan ketentuan: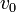 = Kecepatan awal (m/s)
= Kecepatan awal (m/s) = Kecepatan akhir (m/s)
= Kecepatan akhir (m/s)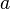 = Percepatan (m/s2)
= Percepatan (m/s2) = Jarak yang ditempuh (m)
= Jarak yang ditempuh (m)
[sunting]Gerak vertikal ke atas
Benda dilemparkan secara vertikal, tegak lurus terhadap bidang horizontal ke atas dengan kecepatan awal tertentu. Arah gerak benda dan arah percepatan gravitasi berlawanan, gerak lurus berubah beraturan diperlambat.Peluru akan mencapai titik tertinggi apabila Vt sama dengan nol.
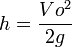
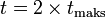
 Keterangan:
Keterangan:- Kecepatan awal= Vo
- Kecepatan benda di suatu ketinggian tertentu= Vt
- Percepatan /Gravitasi bumi: g
- Tinggi maksimum: h
- Waktu benda mencapai titik tertinggi: t maks
- Waktu ketika benda kembali ke tanah: t
[sunting]Gerak jatuh bebas
Benda dikatakan jatuh bebas apabila benda:- Memiliki ketinggian tertentu (h) dari atas tanah.
- Benda tersebut dijatuhkan tegak lurus bidang horizontal tanpa kecepatan awal.
Selama bergerak ke bawah, benda dipengaruhi oleh percepatan gravitasi bumi (g) dan arah kecepatan/gerak benda searah, merupakan gerak lurus berubah beraturan dipercepat.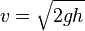
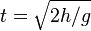 Keterangan:
Keterangan:- v = kecepatan di permukaan tanah
- g = gravitasi bumi
- h = tinggi dari permukaan tanah
- t = lama benda sampai di tanah
[sunting]Gerak vertikal ke bawah
Benda dilemparkan tegak lurus bidang horizontal arahnya ke bawah.Arah percepatan gravitasi dan arah gerak benda searah, merupakan gerak lurus berubah beraturan dipercepat.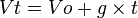
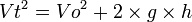 Keterangan:
Keterangan:- Vo = kecepatan awal
- Vt = kecepatan pada ketinggian tertentu dari tanah
- g = gravitasi bumi
- h = tinggi dari permukaan tanah
- t = waktu
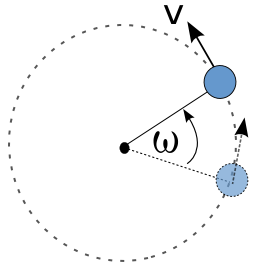
[sunting]Gerak melingkar
Gerak dengan lintasan berupa lingkaran.Dari diagram di atas, diketahui benda bergerak sejauh ω° selama sekon, maka benda dikatakan melakukan perpindahan sudut.Benda melalukan 1 putaran penuh. Besar perpindahan linear adalah
sekon, maka benda dikatakan melakukan perpindahan sudut.Benda melalukan 1 putaran penuh. Besar perpindahan linear adalah atau keliling lingkaran. Besar perpindahan sudut dalam 1 putaran penuh adalah
atau keliling lingkaran. Besar perpindahan sudut dalam 1 putaran penuh adalah 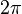 radian atau 360°.
radian atau 360°.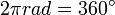

[sunting]Perpindahan sudut, kecepatan sudut, dan percepatan sudut
Perpindahan sudut adalah posisi sudut benda yang bergerak secara melingkar dalam selang waktu tertentu. Keterangan:
Keterangan: = perpindahan sudut (rad)
= perpindahan sudut (rad) = kecepatan sudut (rad/s)
= kecepatan sudut (rad/s)- t = waktu (sekon)
Kecepatan sudut rata-rata ( ): perpindahan sudut per selang waktu.
): perpindahan sudut per selang waktu. Percepatan sudut rata-rata (
Percepatan sudut rata-rata ( ): perubahan kecepatan sudut per selang waktu.
): perubahan kecepatan sudut per selang waktu.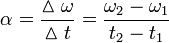
 : Percepatan sudut (rad/s2)
: Percepatan sudut (rad/s2)[sunting]Percepatan sentripetal
Arah percepatan sentripetal selalu menuju ke pusat lingkaran.Percepatan sentripetal tidak menambah kecepatan, melainkan hanya untuk mempertahankan benda agar tetap bergerak melingkar.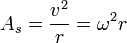 Keterangan:
Keterangan:- r : jari-jari benda/lingkaran
- As: percepatan sentripetal (rad/s2)
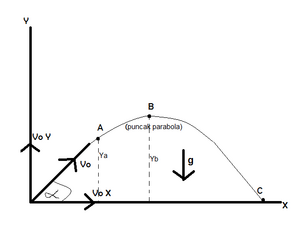
[sunting]Gerak parabola
Gerak parabola adalah gerak yang membentuk sudut tertentu terhadap bidang horizontal. Pada gerak parabola, gesekan diabaikan, dan gaya yang bekerja hanya gaya berat/percepatan gravitasi.Pada titik awal,
 Pada titik A (t = ta):
Pada titik A (t = ta):
 Letak/posisi di A:
Letak/posisi di A: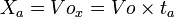
 Titik tertinggi yang bisa dicapai (B):
Titik tertinggi yang bisa dicapai (B): Waktu untuk sampai di titik tertinggi (B) (tb):
Waktu untuk sampai di titik tertinggi (B) (tb):


 Jarak mendatar/horizontal dari titik awal sampai titik B (Xb):
Jarak mendatar/horizontal dari titik awal sampai titik B (Xb):
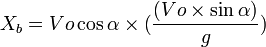
 Jarak vertikal dari titik awal ke titik B (Yb):
Jarak vertikal dari titik awal ke titik B (Yb):
 Waktu untuk sampai di titik C:
Waktu untuk sampai di titik C: Jarak dari awal bola bergerak sampai titik C:
Jarak dari awal bola bergerak sampai titik C:

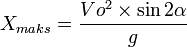














![W = n \times R \times T \times[\ln V_2 - \ln V_1]](http://upload.wikimedia.org/wikibooks/id/math/0/a/7/0a71834fa480baf975b62a9a64bb7b7d.png)



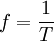









0 komentar:
Posting Komentar